- Published on
在英伟达官网免费使用 SD-XL 文生图 和 Llama3-70b 等 AI 产品
- Authors
- Name
- 三金得鑫
- 掘金
- 掘金
今天在逛英伟达官网的时候,发现在他们网站上可以免费使用各种比较火的开源大模型,包括:
- Chat 对话、推理:Llama-3、Phi-3 等;
- 文生图:sdxl-turbo、stable-diffusion-xl、edify-image、edify-3d-early-access(3D 的喔~);
- 文生视频:Stable-video-diffusion;
尤其是 Stable Diffusion 这个文生图模型,其实很多人的电脑配置都无法达到它运行的最低标准。
大的分类上,平常能用到的就是推理(Reasoning)、视觉设计(Visual Design)和最近趋势(Trending now)。在 Gaming 里还有数字人,不过建模实属简陋,感兴趣的小伙伴可以自行探索,我们主要演示推理和视觉设计。
最近趋势(Trending now)
这个里面就是最近比较火的一些模型,比如 Llama-3、Phi-3 和 Stable Diffusion 等等。以 Phi-3-mini-128k-instruct 为例:
直接问一道经典鸡兔同笼问题:
鸡和兔在一个笼子里,共有35个头,94只脚,那么鸡有多少只,兔有多少只?
回答:
首先,我们知道鸡和兔的头数和脚数总和是35头和94只脚。
设鸡有x只,兔有y只。
根据题意,我们有两个方程:
- x + y = 35 (因为鸡和兔的头数总和是35)
- 2x + 4y = 94 (因为鸡有2头和4脚,兔有2头和4脚,所以总共的头和脚数是94)
我们可以通过方程1解出y = 35 - x。然后将y代入方程2中:
2x + 4(35 - x) = 94
2x + 140 - 4x = 94
-2x = -46
x = 23
现在我们知道鸡有23只。通过方程1,我们可以解出兔的数量:
23 + y = 35
y = 35 - 23
y = 12
所以,鸡有23只,兔有12只。
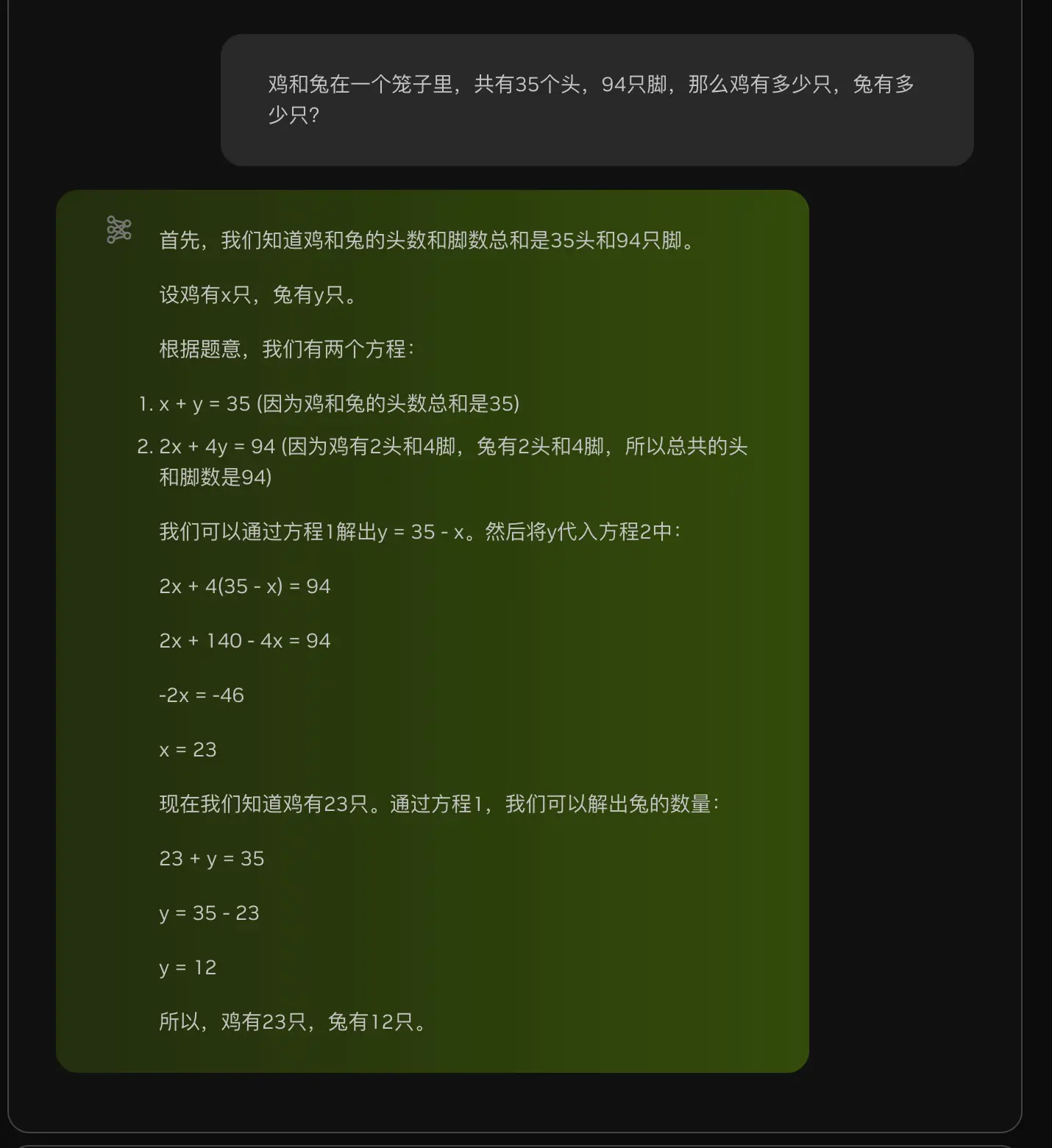
不过再绕一点的逻辑题它的回答是有问题的(原题地址):
你被带到一张桌子前坐了下来,桌子上有一大堆硬币。你还没来得及看清楚桌上到底有多少枚硬币,眼睛就被人蒙上了。这时,有一个声音告诉你,在桌上的硬币里,有二十枚正面朝上,其余的都是反面朝上。现在你可以随意移动桌上的硬币,也可以随意把任意数量的硬币翻面。但你无法通过手指判断某一枚是正面朝上还是反面朝上。
耳边的声音又出现了。他要求你把桌上的硬币分成两堆,在每一堆中,正面朝上的硬币数量必须相等。如果做不到的话,他就一枪打死你。请问,你该怎么做呢?
Phi-3 回答:
首先,我们需要确定整个硬币数量。由于已知正面硬币的数量是20枚,所以总数必然是20+反面面硬币的数量。我们可以通过翻面一些硬币来找到这个数量。
接下来,我们需要找到这个总数的倍数,因为我们需要将硬币划分成两堆,每堆的正面面硬币数量必须相等。这意味着总数必须是两个正面硬币数量的倍数。
我们可以通过翻面一些硬币来找到这个倍数。例如,我们可以翻面一个硬币,如果它变为正面面硬币,那么总数就是21,这是两个正面面硬币数量的倍数(即3的倍数)。如果它变为反面面硬币,那么总数就是19,这也是两个正面面硬币数量的倍数(即19/2=9.5,但是这不是一个整数,所以不能作为倍数)。
继续翻面硬币,直到找到总数是两个正面面硬币数量的倍数的情况。比如,如果总数是30,那么我们可以将硬币划分为两堆,每堆有10个正面面硬币。
最后,将这两堆硬币分别放在两个不同的地方,确保每堆都有相同数量的正面面硬币。这样就满足了题目的要求,并且没有必要杀死。
emmm,没看懂😂
正确答案是:
随便摸出二十枚硬币,把这二十枚硬币都翻个面,然后把它们作为一堆,剩下的所有硬币作为一堆就可以了。
我们来推演一下。首先假设你摸到的硬币里一枚正面朝上的都没有,那就说明那20枚正面朝上的都在另一堆里。现在你把摸到的20枚硬币都翻一次面,它们就全都变成20枚正面朝上的了。20等于20,满足要求。
接下来,我们再假设你摸到的20枚硬币里有一枚正面朝上的,这说明另一堆里还有19枚正面朝上的。现在你把摸到的20枚全部翻面一次,它们就变成了1枚反面朝上、19枚正面朝上。19等于19,满足要求。
一直推演下去,你就会发现,不管你摸到的20枚硬币里有几枚正面朝上,只要把它们翻一次面,最后都可以满足要求。
推理(Reasoning)
我们在 Reasoning 中选择 llam3-70b-instruct 来试试看这道题:
虽然它给我们使用英文回答了,但是它给出的答案是正确的!
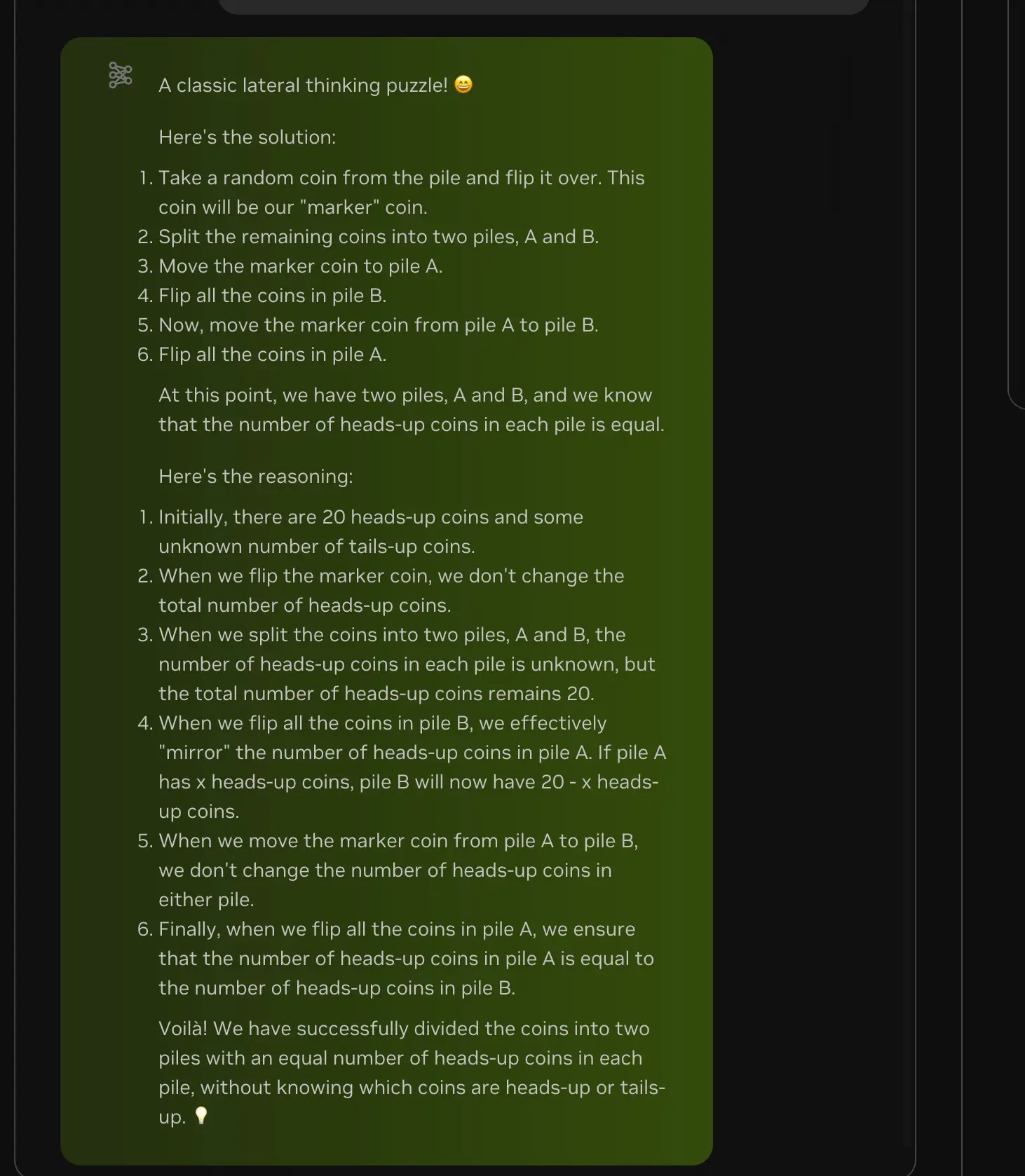
经典的横向思维难题! 😄
这是解决方案:
从一堆硬币中随机取出一枚硬币并将其翻转过来。 这枚硬币将成为我们的“标记”硬币。
将剩余的硬币分成两堆,A 和 B。
将标记硬币移至 A 堆。
翻转 B 堆中的所有硬币。
现在,将标记硬币从 A 堆移动到 B 堆。
翻转 A 堆中的所有硬币。
此时,我们有两堆,A和B,并且我们知道每堆中的单挑硬币数量是相等的。
原因如下:
最初,有 20 个正面朝上的硬币和一些数量未知的背面朝上的硬币。
当我们翻转标记硬币时,我们不会改变正面硬币的总数。
当我们将硬币分成 A 和 B 两堆时,每堆中正面硬币的数量是未知的,但正面硬币的总数仍然是 20。
当我们翻转 B 堆中的所有硬币时,我们实际上“镜像”了 A 堆中单挑硬币的数量。如果 A 堆有 x 个单挑硬币,则 B 堆现在将有 20 - x 个单挑硬币。
当我们将标记硬币从 A 堆移动到 B 堆时,我们不会改变任一堆中正面硬币的数量。
最后,当我们翻转A堆中的所有硬币时,我们确保A堆中正面硬币的数量等于B堆中正面硬币的数量。
瞧! 我们成功地将硬币分成两堆,每堆中正面朝上的硬币数量相同,但不知道哪些硬币是正面朝上的,哪些硬币是反面朝上的。 💡
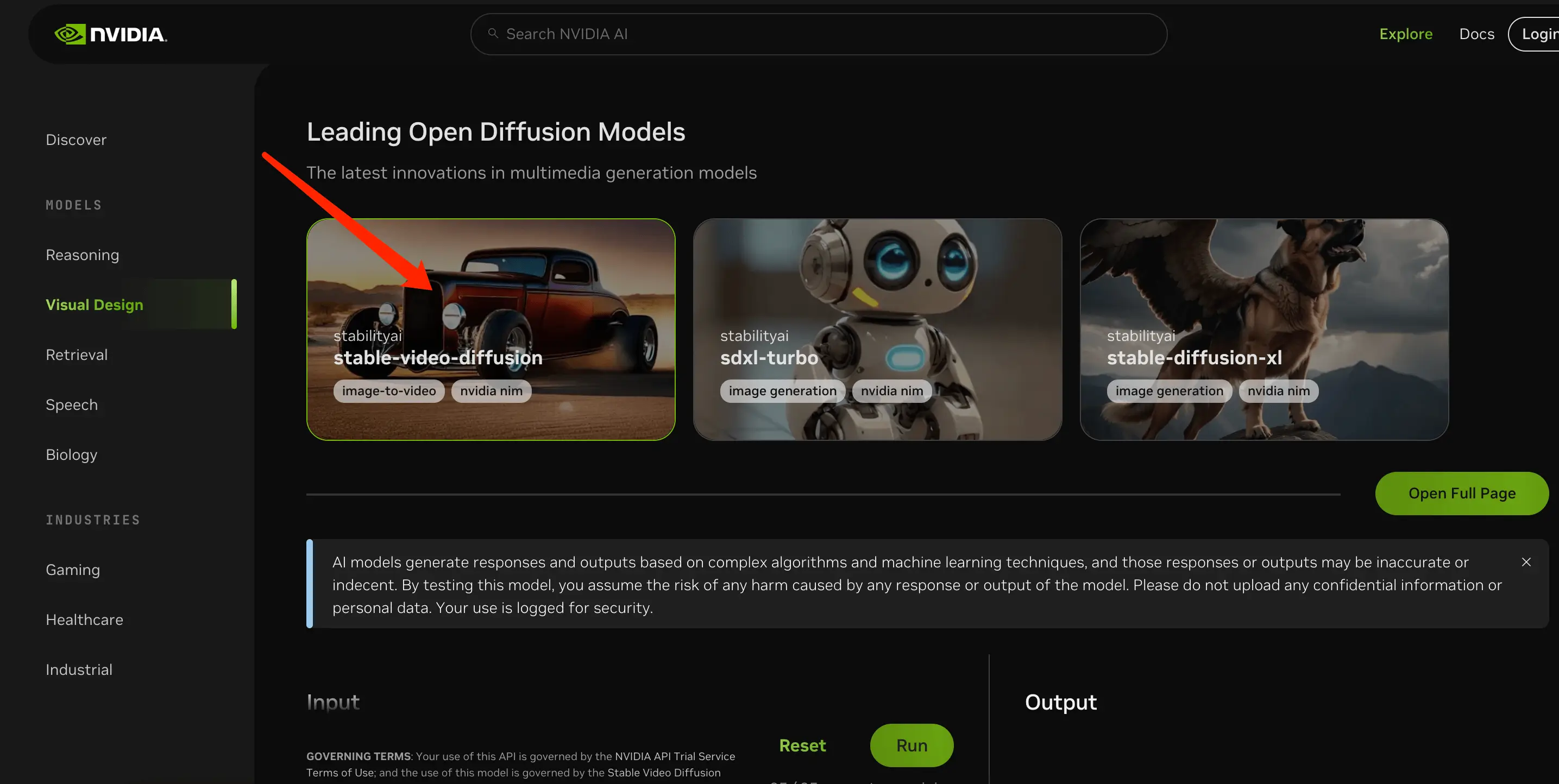
视觉设计(Visual Design)
在视觉设计中,我们平常可以用到就是文生图 Stable Diffusion 模型了,以 sdxl-turbo 和 stable-diffusion-xl 这两个模型为例来生成图片看看:
提示词:A girl,Round face, slightly bend and lower head + pale red lips
, ambient light, extremely detailed, best quality, 8k HD.
sdxl-turbo
stable-diffusion-xl
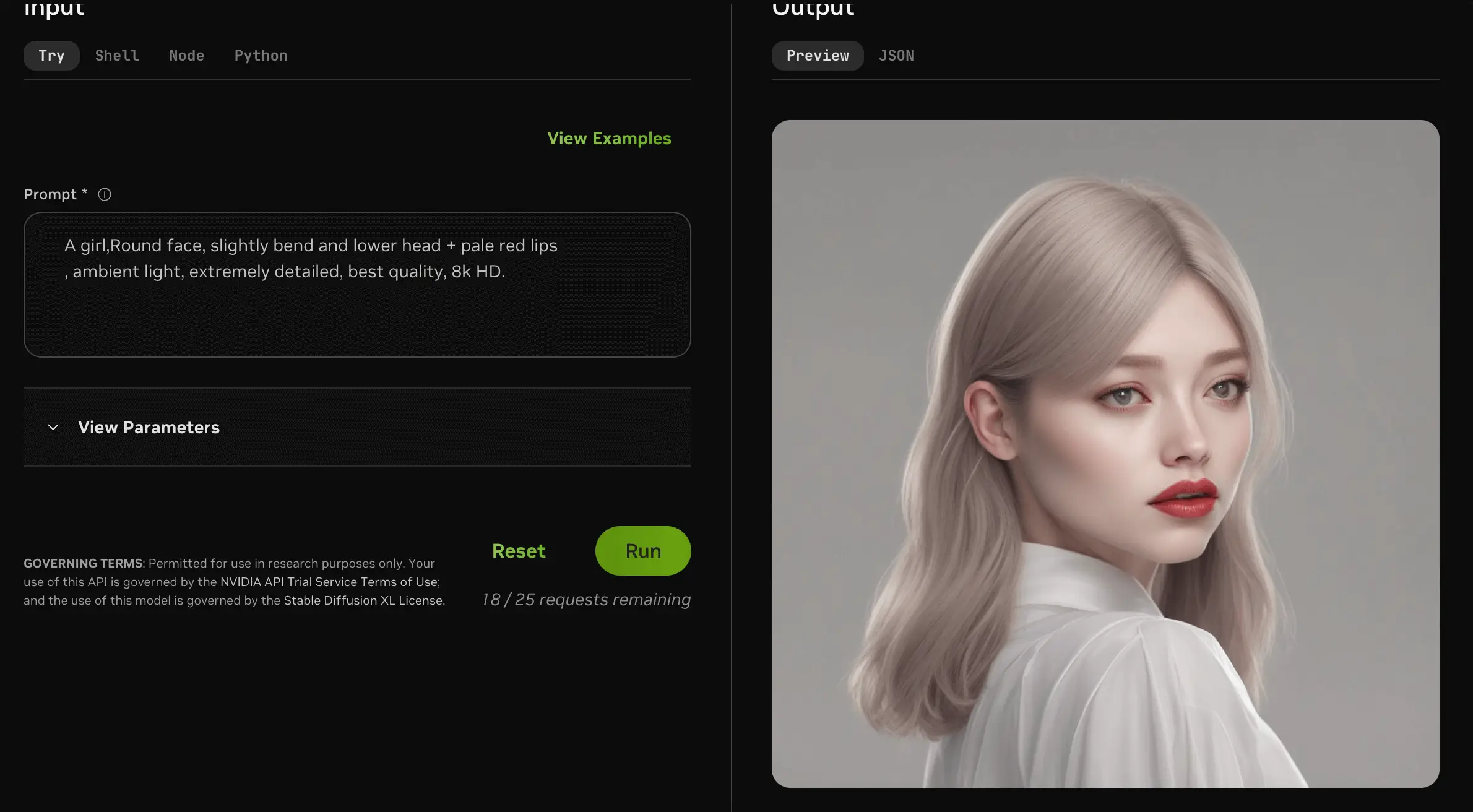
如图,sdxl_turbo 胜出🏆。文生图模型因为比较消耗资源的原因,对于访客只提供了 25 次调用的机会。
stable-video-diffusion
接下来我们试试 stable-video-diffusion 试试图生视频,提供一张今天在咖啡店拍的照片:

上传图片并开始 run 起来,大概有个十来秒就生成了一个 4s 的视频:
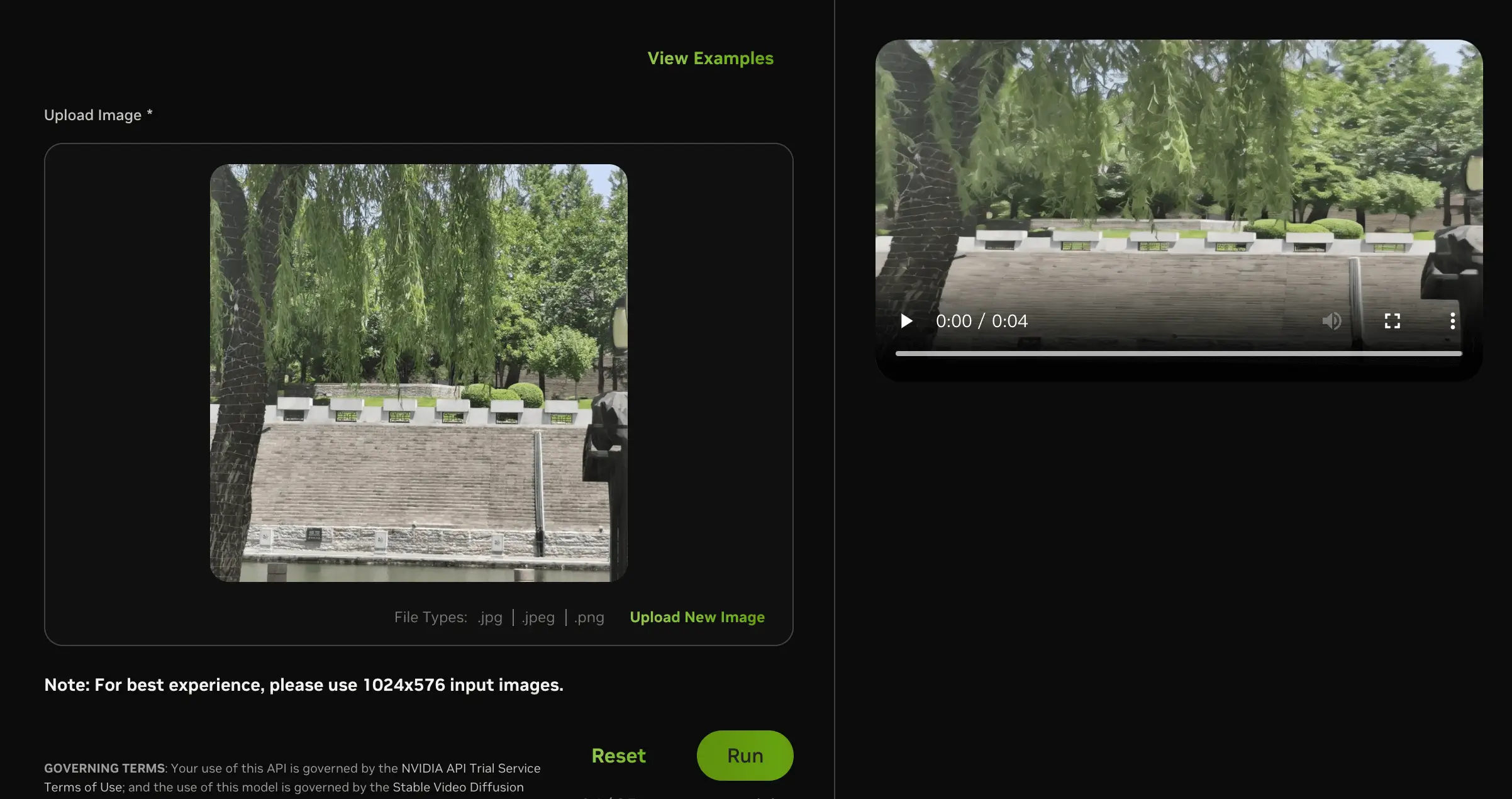
视频在这里:stable_video
生成的视频有点高糊而且卡顿,但是免费的还要什么自行车呢~
感兴趣的小伙伴可以去试试看😁